Mathematics applied to
Mathematical models may be able to describe the complex interactions present in tumor growth and other medical problems and provide insight and tools to design novel therapies and optimize current ones.
What is Mathematical Oncology?
Mathematical Oncology describes processes in oncology using the tools and systematization methods of Mathematics. This includes mathematical model building and techniques from Applied Mathematics: differential equations, numerical methods, optimization, etc.
In other fields of Science such as Physics or Engineering, scientists write equations and pose problems in a language familiar to the mathematician. However, in Medicine it is the applied mathematician who must understand the problem and formulate models in partnership with biologists and/or clinicians, which makes the field truly interdisciplinary and demands people with a strong interest in applications.
The ultimate goals are to improve the current treatments of cancer patients and to build hypotheses that can be tested by clinicians and biologists. Thus, we try to generate knowledge directly applicable in Medicine.
What is MOLAB?
The Mathematical Oncology Laboratory (MOLAB) is a multidisciplinary research group developing mathematical studies on cancer-related problems. The collaboration between different researchers together with with medical doctors provides new perspectives and understanding in oncology.
We capture and implement the fundamental aspects of cancer, and other diseases, in our mathematical models. We feed these models with patient data, and simulate their behavior in a realistic way, opening a virtual window that allows us to observe tumors in a way that would not be possible in real life.
Our purpose is to go beyond mathematical models. We want them to have a real impact on patients: improving the diagnosis of cancer, anticipating its evolution, and identifying treatment schedules ameliorating current standards.
Cancer treatments and therapeutic interventions are subject to a great deal of uncertainty and involve a fair amount of trial and error. This reduces the potential clinical benefits and causes costs to shoot up. The outcome from currently available treatments can be improved, for instance by optimizing schedules, dosages, and combinations. Clinical trials could be designed virtually to produce better results with lower investment, what is referred to as in silico trials. This allows us to achieve optimal results in terms of patient survival and treatment toxicity.
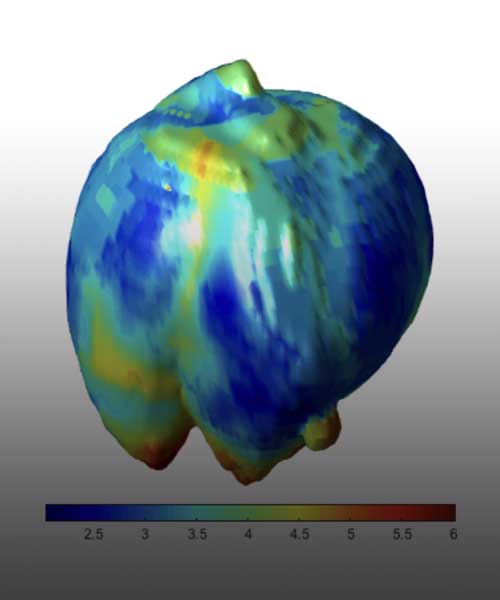
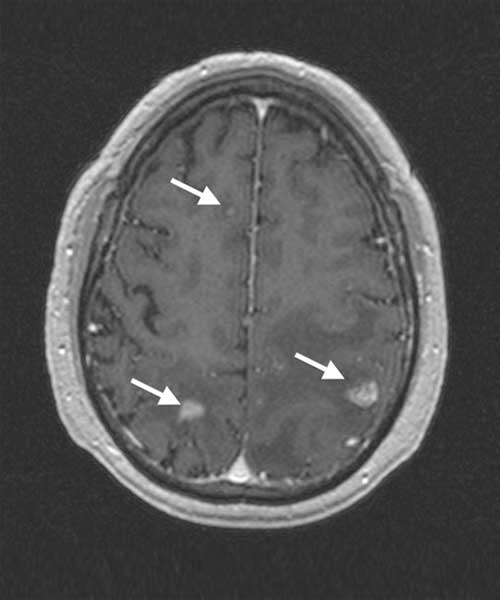
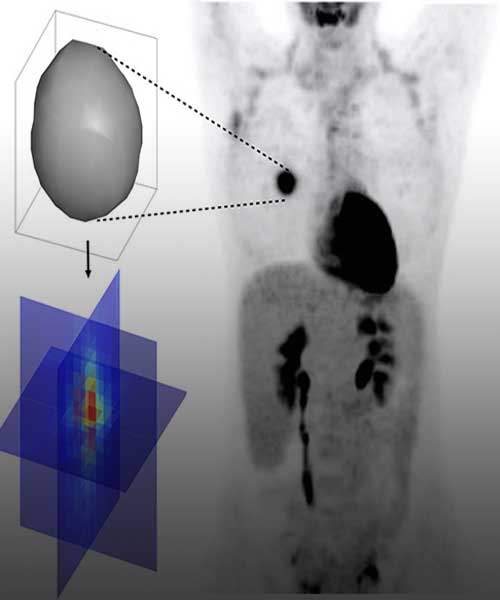
An increasing amount of data from cancer patients is available through different ‘omics’ technologies (genomics, proteomics, transcriptomics, etc.), as well as medical imaging like Magnetic Resonance (MRI) or Positron Emission Tomography (PET). We integrate these data with mathematical models to identify patterns that can serve as biomarkers of prognosis and response. For instance, we develop imaging biomarkers from MRI morphological features associated to the survival of patients with brain metastases. Other examples are topological features in flow cytometry data from leukaemia patients or metabolic footprints of cancer metabolism in PET images. These features provide prognostic tools that aid in patient stratification and are a step towards personalized precision medicine.
The immune system is the complex set of biological defenses that fight infections and other diseases such as cancer. Many aspects of the immune system are not yet completely understood and mathematical models shed light on how the different subsystems interact and develop specific immune responses. However, the immune system does not always eliminate tumor cells, as these develop mechanisms to evade it. Immunotherapies stimulate the immune system to increase the body’s antitumor response. Mathematical models help in understanding the details of the actions of immunotherapies, in developing image-based biomarkers of response, and in designing more effective therapeutic approaches.
Mathematical models based on ordinary or partial differential equations, as well as individual-based discrete models, describe biological processes of relevance in cancer: tumor growth, radiotherapy, chemotherapy, interactions in the microenvironment, the role of the vasculature, etc. Studying theoretically these models may help in better understanding their applicability and potential to describe clinical scenarios. Developing new computational methodologies able to describe cancer growth and response to treatments can be helpful to design clinical studies in silico.
The heterogeneous population of cells conforming malignant tumors is the result of Darwinian evolution and selection. There is yet much to unveil about these processes, which are key to understanding tumor aggressiveness, response to therapy and the emergence of resistance. We study evolutionary dynamics from a twofold perspective: theoretical and practical. For the first, we work with discrete and continuous phenotypically structured mathematical models to describe phenotypic instability and evolvability. For the latter, we use medical imaging and clinical data to study metabolic scaling laws arising in human cancers.
Evolutionary
dynamics
An ever-increasing amount of data is available in biomedical research. In MOLAB, years of joint work with medical doctors have led to the creation of big databases of medical data from patients of solid tumors and leukemias, as well as other diseases such as diabetes. We work with medical images (MRI and PET), flow cytometry, histopathology, genetic alterations, etc. These data are scrutinized using dimensionality reduction and techniques like Topological Data Analysis (TDA) or Machine Learning. We advocate preserving the interpretability and identifiability of our models and connecting as much as possible the results to mechanistic modelling.