Tuesday, January 31, Seminar , 11:30h. Salón de Grados E.T.S.I.Industriales

Álvaro G. López

Nonlinear Dynamics, Chaos and Complex Systems Group

Departamento de Física

Universidad Rey Juan Carlos

Tulipán s/n,

28933 Móstoles, Madrid, Spain

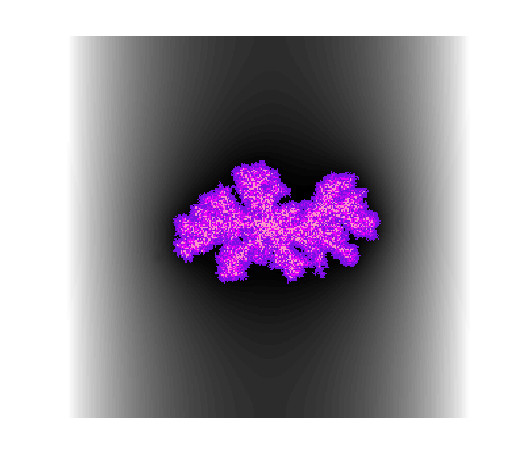
In this talk, we present our work in the mathematical modeling of tumor-immune interactions [1, 2]. In particular, this study uses in silico experiments and mathematical analyses to characterize the dynamics of the cytotoxic cell-mediated immune response to tumor growth, in the limit of very efficient immune responses. A stochastic hybrid cellular automaton model is developed, describing the spatiotemporal evolution of the tumor as the effector T-cells lyse it. The model parameters are adjusted to an ordinary differential equation model, which has been previously validated with experimental data obtained from in vivo experiments and chromium release assays [1, 3]. We utilize the cellular automaton model to investigate the decay rate of the tumor, depending on its morphology. More specifically, the constant rate of the decay is related to the box-counting dimension of the tumor’s boundary, confirming a power-law relation between the fractal dimension of the tumor and the lytic rate [2].

[1] Álvaro G. López, Jesús M. Seoane, and Miguel A. F. Sanjuán. Destruction of solid tumors by immune cells. Commun. Nonlinear Sci. Numer. Simulat. 44, 390-403, 2017. (https://doi.org/10.1016/j.cnsns.2016.08.020)

[2] Álvaro G. López, and Lorena R. Sanjuán. A scaling law relating the rate of destruction of a solid tumor and the fractal dimension of its boundary. Submitted to Fractals,  2022. (https://doi.org/10.1101/2022.06.29.498072)

[3] Álvaro G. López, Jesús M. Seoane, and Miguel A. F. Sanjuán. A validated mathematical model of tumor growth including tumor-host interaction, cell-mediated immune response and chemotherapy. Bull. Math. Biol. 76, 2884-2906, 2014. (https://doi.org/10.1007/s11538-014-0037-5)