Publication
On the Dynamics and Optimal Control of a Mathematical Model of Neuroblastoma and its Treatment: Insights from a Mathematical Model
José García Otero, Mariusz Bodzioch, and Juan Belmonte-Beitia
M3AS: Mathematical Models and Methods in Applied Sciences 07(34) (2024)
MOLAB authors
Abstract
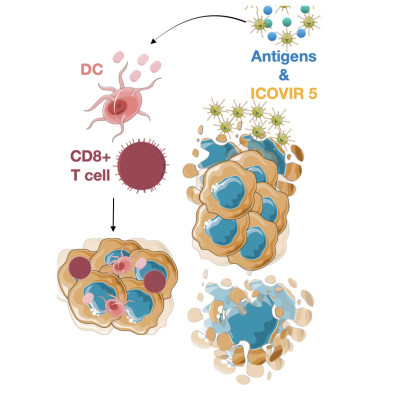
Celyvir is an advanced therapy medicine, which consists of mesenchymal stem cells (MSCs) containing the oncolytic virus ICOVIR 5. This article presents a dynamic system that attempts to capture the fundamental relationships between cancer, the immune system and adenoviruses. Two forms of treatment have been studied: continuous and periodic, the second being the more realistic. In the analysis of the first model, in addition to identifying the critical points, their properties and bifurcation points, different numerical simulations has been carried out. In this way, it has been shown that there are bistability regimes in which Celyvir can induce an equilibrium of tumour progression, or tumour-free. A sensitivity analysis has also been performed to see which parameters are the most relevant in the system. Subsequently, an optimal control problem with non-linear objective functional has been formulated, where the therapeutic goal is not only to minimize the size of the tumour cell population and the total cost of treatment, but also to prevent the tumour from reaching a critical size. It has been shown that the optimal control is bang-bang. With the second model, a threshold value of viral load has been identified at which the success of the treatment could be ensured. It is clear in both models that a low viral load would lead to a relapse of the disease. Finally, it has been shown that a periodic bang-bang regimen should be used to optimize treatment with Celyvir.