Publication
CAR T cells for T-cell leukemias: Insights from mathematical models
V.M. Pérez-García, O. León-Triana, M. Rosa, A. Pérez-Martínez
Comm Nonlin Sci Numer Simul, 96, 105684 (2021)
MOLAB authors
Abstract
Immunotherapy has the potential to change the way all cancer types are treated and cured. Cancer immunotherapies use elements of the patient immune system to attack tumor cells. One of the most successful types of immunotherapy is CAR-T cells. This treatment works by extracting patient’s T-cells and adding to them an antigen receptor allowing tumor cells to be recognized and targeted. These new cells are called CAR-T cells and are re-infused back into the patient after expansion in-vitro.
This approach has been successfully used to treat B-cell malignancies (B-cell leukemias and lymphomas). However, its application to the treatment of T-cell leukemias faces several problems. One of these is fratricide, since the CAR-T cells target both tumor and other CAR-T cells. This leads to nonlinear dynamical phenomena amenable to mathematical modeling.
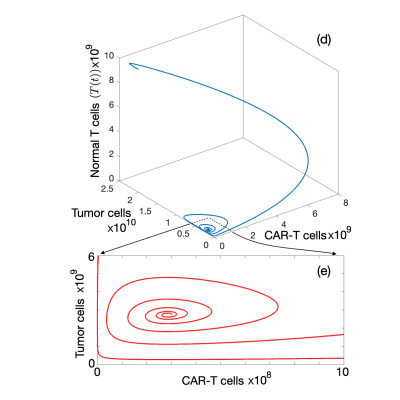
In this paper we construct a mathematical model describing the competition of CAR-T, tumor and normal T-cells and studied some basic properties of the model and its practical implications. Specifically, we found that the model reproduced the observed difficulties for in-vitro expansion of the therapeutic cells found in the laboratory. The mathematical model predicted that CAR-T cell expansion in the patient would be possible due to the initial presence of a large number of targets. We also show that, in the context of our mathematical approach, CAR-T cells could control tumor growth but not eradicate the disease.