Belmonte Beitia, Juan. Pérez García, Victor M.. Rojas, Clara. 

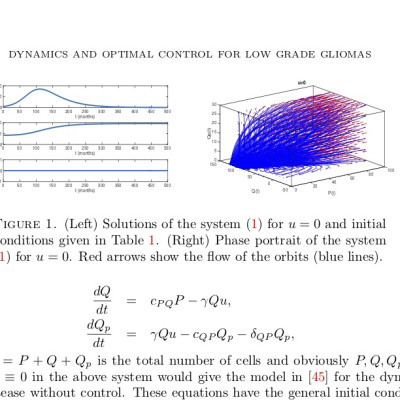
We discuss the optimization of chemotherapy treatment for low-grade gliomas using a mathematical model. We analyze the dynamics of the model and study the stability of solutions. The dynamical model is incorporated into an optimal control problem for which different objective functionals are considered. We establish the existence of optimal controls and give a detailed discussion of the necessary optimality conditions. Since the control variable appears linearly in the control problem, optimal controls are concatenations of bang-bang and singular arcs. We derive a formula of the singular control in terms of state and adjoint variables. Using discretization and optimization methods we compute optimal drug protocols in a number of scenarios. For small treatment periods, the optimal control is bang-bang, whereas for larger treatment periods we obtain both bang-bang and singular arcs. In particular, singular controls illustrate the metronomic chemotherapy.